之前只知道浮点数存在精度问题,但是不理解为什么。现在通过维基百科学习了,在此记录下来。
浮点数的格式
浮点数是按照 符号位 + 指数位 + 小数位 来存储的。按照位数的不同,分为单精度浮点数和双精度浮点数。
单精度浮点数(float/single)

单精度浮点数的第 1 位是符号位。后面 8 位是指数部分,用 e 表示。指数部分按照 IEEE 754 binary32 标准可以是有符号或者无符号数(补码)。如果是有符号数,则取值范围是 -128~127;如果是无符号数,则取值范围是 0~255(全0和全1按照标准被保留),并且需要减去一个 127 的偏移量,所以取值范围是 -126~127。再后面 23 位是小数位。所以一个 32 位的浮点数的十进制值为:
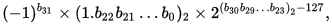
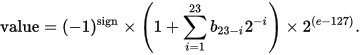
以上图这个单精度浮点数为例,它的计算过程如下:
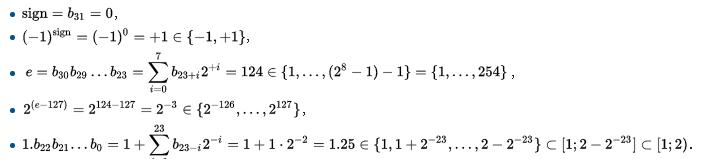
双精度浮点数(double)
双精度浮点数的第 1 位是符号位,后面 11 位是指数位,再后面 52 位是小数位。
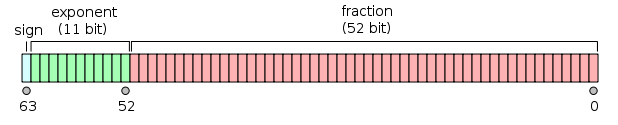
精度和取值范围
很显然,精度是由小数位数决定,而取值范围是由指数范围决定。
对于单精度浮点数,23 位小数部分其十进制值是 8388608,所以十进制的精度就是 6~7 位。8 位指数部分,由前面的描述可知 e 的取值范围是 -126~127,小数部分取值是 1~2(不包含2),所以对应的十进制范围大概是 -3.402823e38~3.402823e38。
对于双精度浮点数,精度 15~16 位。取值范围大概是 -1.79769e308~1.79769e308。
下面这个是单精度和双精度浮点数的详细精度范围:
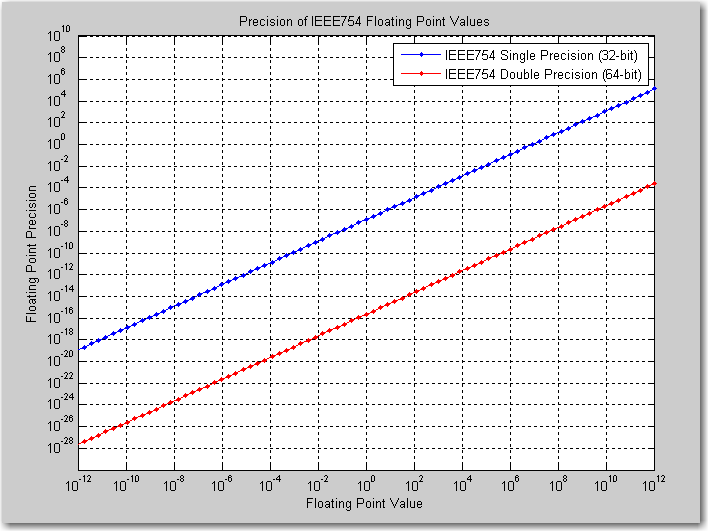
单精度浮点数的精度问题
首先,浮点数的位级表示是二进制的科学计数法,而单精度浮点数小数点后面的位数是 23 位,超过 23 位就无法表示了。所以浮点数是一个“有损”格式。
举个例子,0.1的二级制为0.000110011001100[1100]...,所以当你写下float f = 0.1f时,在计算机的内存中的f已经不是0.1了,而是一个非常接近0.1的值。意识到这一点很重要。
引起浮点数的精度问题的除了小数点后面的位数,还有浮点数的舍入(rounding)。
舍入操作是位级操作。编程语言中的浮点数舍入遵循首先向最近舍入,然后向偶数舍入。
比如有个二进制小数10.01,现在保留小数点后一位小数,则得到10.0。
-------|-------|-------|-----
10.0 10.01 10.1
可以看到,10.01恰好在10.0和10.1正中间,所以向偶数舍入,结果是10.0。
除了像0.1这样的小数存在浮点数精度问题,整数也有,但是在一定范围内的整数转换为浮点数却是可以不损失任何精度的。
对于一个 32 位的整数,只要它的二进制形式小于等于 24 位有效数字(浮点数有一位隐藏位),那么这个整数可以无损转换为单精度浮点数。
我们来算一下这个整数是多大:224 - 1 = 16777215。
实际上,224 = 16777216 也是可以无损转换为一个单精度浮点数的,因为它的位级表示是 1 后面一串 0。
所以我们有一个直观的感觉,int 转换为 float 如果想要无损,那么这个 int 不能超过一千六百多万。 当然了,并不是大于 16777216 的 int 一定不能无损转换为 float,只要位级表示在浮点数的精度范围内,就是可以无损的。
参考资料:
转载请注明出处:
This work is licensed under a MIT License.