数字的补码

补数计算法（Method of complements）

首先，网上流传的“补码”一般是指二进制补码，而这里说的是广义的“补码”，或者“补数”。我们说一个数字的时候，必须明确这个数字是什么进制的。比如 12345₁₀，对于常用的十进制数，一般都会把下标省去。

那么，我们如何算出 12345 的补数（Nines’ complement）？用每一位都是 9 的数按位相减：

    99999
-   12345 （目标数）
----------
    87654 （目标数的补数）

补数的意义是什么？补数的意义就在于，用加法计算减法。比如计算 123 - 45：

    123 (x)
-    45 (y)
--------------------
    123 (x)
+   954 (999 - y)
--------------------
   1077 (x + 999 - y)

舍去最高位的进位：

    077 (x + 999 - y - 1000 = x - y -1)

加上 1 就是所得结果：

    078 (x - y)

计算机如何存储有符号数

人类使用十进制数字的时候，会在数字前面加一个 - 来表示负数，但是计算机只能用“位串”来表示数字，所以历史上出现过多种方式来表示有符号数。

按照维基百科的介绍，有如下几种二进制有符号数的表示法，其中有的方法已经过时了：

• 有符号模表示法（Signed magnitude representation）
• 反码表示法（Ones’ complement）
• 补码表示法（Two’s complement）
• Excess-K
• Base −2
• Google’s Protocol Buffers zig-zag encoding

其中，Ones’ complement 和上面举例说明的 Nines’ complement 相似，就是用全是 1 的位串按位减去目标数的每一位，这个结果和把目标数的每一位按位取反是一样的，所以 Ones’ complement 又称“反码”。

    1111
-   1010 （目标数）
---------
    0101 （目标数的反码）

很多早期的计算机使用反码表示法，但是绝大部分的现代计算机都使用后面描述的表示法了。

二进制补码

二进制补码是现在使用最广泛的有符号数表示法。对于一个 n 位的二进制数 a_n-1a_n-2…a₀，它的值为：

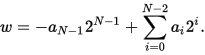
二进制有符号数的第一位（MSB）是符号位，0 表示正数，1 表示负数。用补码可以表示的数值范围是：-2^n-1 ~ 2^n-1-1，所以一个 8 位有符号数的范围是 -128~127。

如何计算补码

正数和 0 的补码就是其本身。计算一个 n 位负数的补码有两种方法：

• 首先计算反码，然后反码加 1，得到补码
• x_补=2ⁿ-|x|，这个公式里面用的是无符号数

参考资料：

• Method of complements
• Signed number representations
• Ones’ complement
• Two’s complement

• ← Previous Post
• Next Post →