Unity 渲染 Shader

渲染所需的数学知识

Posted by QXSoftware on October 27, 2016

Unity Shader 编写所必须的基础数学知识

笛卡尔坐标系（Cartesian Coordinate System）

我们平时使用的坐标系就是笛卡尔坐标系，它分为左手坐标系和右手坐标系。Unity 使用的是左手坐标系。

向量

点积（Dot Product）

两个向量的点积的结果是一个标量。

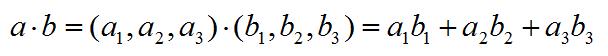
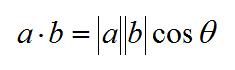
叉积（Cross Product）

两个向量的叉积是一个垂直于这两个向量的向量。这个向量的方向和使用左手坐标系还是右手坐标系有关。

矩阵（Matrix）

矩阵基本性质

  • 不满足交换律

    AB ≠ BA

  • 满足结合律

    ABCD = A(BC)D = AB(CD)

特殊的矩阵

  • 方阵 行数和列数相等的矩阵叫做方阵（Square Matrix），渲染常用的是 3x3 和 4x4 矩阵。如果除了对角线之外的元素都是 0，那么这个矩阵也叫做对角矩阵（Diagonal Matrix）。

    方阵：

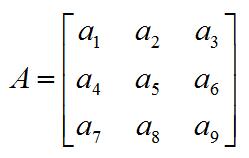
    对角矩阵：

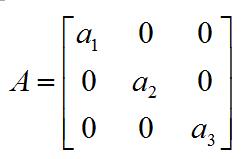
  • 单位矩阵 单位矩阵（Identity Matrix）是对角线的元素都为 1 的对角矩阵。单位矩阵一般用 I 表示。

    MI = IM

    单位矩阵：

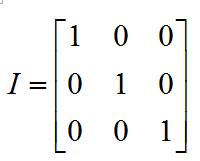
  • 转置矩阵 转置矩阵（Transpose Matrix）就是将一个 mxn 的矩阵翻转过来变成 nxm 的矩阵。

    转置矩阵：

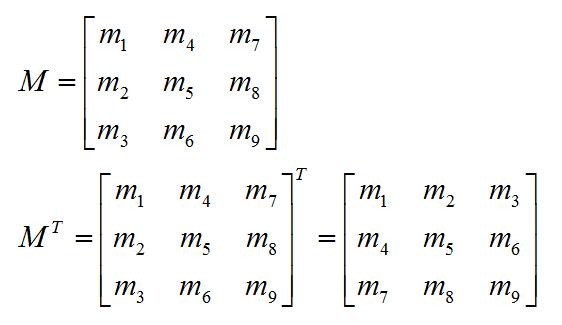
    转置矩阵的性质：

    • 转置的转置就是它本身

      (MT)T = M

    • 矩阵乘积的转置，等于各矩阵转置的逆序乘积

      (ABCD)T = DTCTBTAT

  • 逆矩阵 首先，并不是所有的矩阵都有逆矩阵（Inverse Matrix）。矩阵 M 存在逆矩阵 M-1 的前提之一就是，M 必须是一个方阵。M 和 M-1 相乘得到单位矩阵：

    MM-1 = M-1M = I

    逆矩阵有以下性质：

    • 一个可逆矩阵的逆矩阵的逆矩阵是它本身

      (M-1)-1 = M

    • 单位矩阵的逆矩阵还是单位矩阵

      I-1 = I

    • 转置的逆矩阵是逆矩阵的转置

      (MT)-1 = (M-1)T

    • 矩阵乘积的逆等于反向逆矩阵的乘积

      (ABCD)-1 = D-1C-1B-1A-1

  • 正交矩阵 正交矩阵（Orthogonal Matrix）是方阵。如果 M 和 MT 的乘积是单位矩阵的话，则 M 是正交的。

    MMT = I

    这等价于，M 的逆矩阵等于转置矩阵。

    M-1 = MT

正交矩阵的条件：

  • 每一行都是单位矩阵
  • 每一行之间都相互垂直

正交矩阵由一组标准正交基构成。

在 Unity 中，旋转矩阵是正交矩阵，包含统一缩放比的缩放矩阵除以缩放系数 k 之后也是正交矩阵。

行向量还是列向量？

首先要明确的是，Unity Shader 中使用的是列向量。

列向量：

列向量

行向量：

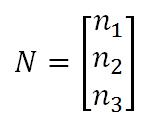
行向量

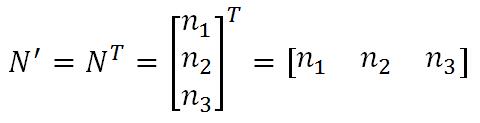
行向量和列向量与矩阵相乘的结果是不一样的，所以必须事先清楚用的是行向量还是列向量。

行向量相乘：

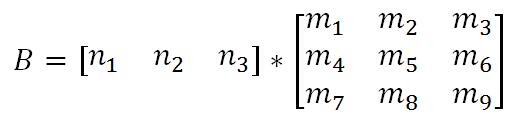
列向量相乘：

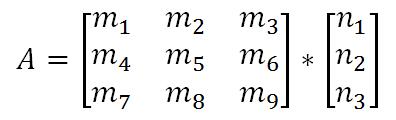
由于 Unity 使用列向量，所以一般情况下，矩阵乘法都是右乘，例如将顶点坐标从模型空间变换到裁剪空间：

o.pos = mul(UNITY_MATRIX_MVP, v.position);

或者将矩阵转置一下，用行向量乘法也是一样的：

o.pos = mul(v.position, transpose(UNITY_MATRIX_MVP));

空间变换（Transform）

上面总结了矩阵的各种知识点，其实矩阵的意义就在于空间变换。

线性变换

线性变换（Linear Transformation）的定义是，在线性空间 V 上的一个变换 A 称为线性变换，如果对于 V 中任意的元素 α，β 和数域 P 中任意 k，都有：

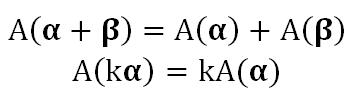
典型的线性变换包括：缩放、旋转等。对于线性变换，我们只需要用一个 3x3 的矩阵就可以表示。平移不是线性变换。为了用矩阵表示平移，需要增加一个维度，这时就有了齐次坐标（Homogeneous Coordinate）。

将线性变换和平移变换用一个矩阵表示，这就是仿射变换（Affine Transformation），这是一个 4x4 的矩阵：

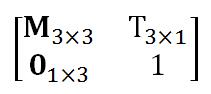
其中 T3x1 表示平移，M3x3 表示缩放和旋转的乘积。

坐标空间转换

给定一个空间 P，和子空间 C，现在知道子空间的坐标轴在 P 中的表示：xc，yc，zc，则从 C 到 P 的转换矩阵为：

Mc→p = [xTc yTc zTc]

变换组合

当我们想要表现一系列变换时，通常要按照一定顺序依次执行。由于矩阵满足结合律，所以可以将所有变换矩阵相乘得到一个矩阵。用这个矩阵去变换和依次变换的效果是一样的。

Unity 处理变换的惯例是TRS（Translate Rotate Scale），实际的顺序是：缩放、旋转、平移。常用的 API 例如：

public static Matrix4x4 TRS(Vector3 pos, Quaternion q, Vector3 s);

转载请注明出处：

This work is licensed under a MIT License.